Mastering RSA Cryptography: From Mathematical Theory to Python Implementation

Explore the RSA Cryptography Algorithm and the significance of prime numbers, Euler's Totient Funct...

ThefCraft
12 min · Jun 17, 2024
947
315

Mastering RSA Cryptography: From Mathematical Theory to Python Implementation

rsa

rsa

Introduction

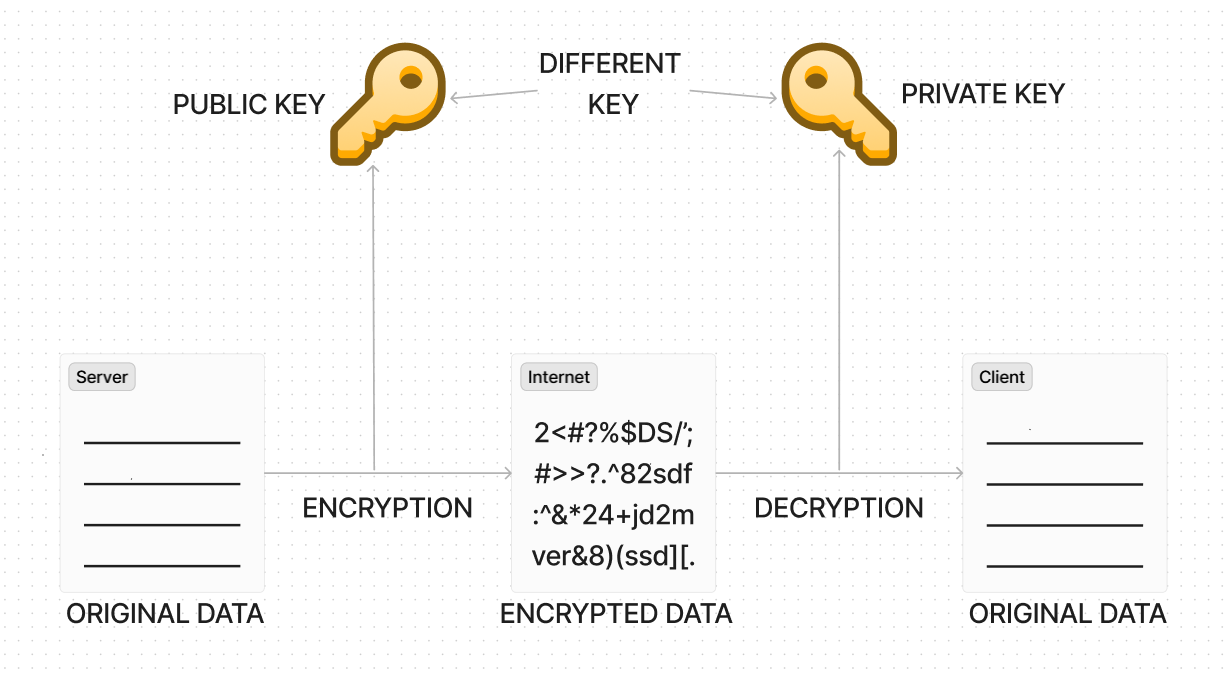
What RSA is? RSA is a Cryptography Algorithm Which is widely used method for encrypting and decrypting messages. It is named after its creators, Ron Rivest, Adi Shamir, and Leonard Adleman, who developed it in 1977. It is based on the difficulty of factoring large numbers, and it is widely considered to be a secure method for encrypting data.

In this article, I will implement the RSA algorithm from scratch in Python while discussing its underlying mathematical theory.

Section 1: Understanding RSA Encryption

To understand how the RSA algorithm works, we first need to understand the concept of public and private keys. In the RSA algorithm, each and every user possesses a pair of keys: a public key and a private key. The public key is shared with anyone who wishes to send a message to the user, and it is used for encryption. The private key remains confidential and is used for decryption.

Here’s an example of how the RSA algorithm works:

  • Imagine Alice wants to send a message to Bob. He first encrypts the message using Bob's public key.
  • The encrypted message is then sent to Bob.
  • Upon receiving the encrypted message, Alice uses her private key to decrypt the message and read the original content.

Do you wonder why decryption without the public key is impossible?

• • •

Section 2: Mathematical Foundations of RSA

Let's delve into the mathematics behind RSA:

We have to generate some numbers to generate keys

  • Let's Generate two distinct very large prime numbers p and q.
  • Let n be the product of p and q i.e., n = p × q
  • Calculate the phi of n i.e., φ(n) = (p-1) × (q-1).

What is Euler's Phi Function φ(n)

Euler's Phi Function Sometimes knowns as Euler's Totient Function counts the number of positive integers that are less than or equal to n and are coprime to n. i.e., the greatest common divisor (gcd) of n and each of these integers is equal to one.

for example, the totient of 9 is 6 because the totatives of 9 are 1, 2, 4, 5, 7 and 8 and number of totatives of 9 is 6 so totient of 9 is 6.

Then, \[ \phi(n) = n \times \left(1 - \frac{1}{p_1}\right) \times \left(1 - \frac{1}{p_2}\right) \times \ldots \times \left(1 - \frac{1}{p_k}\right) \] Where p1, p2, ...., pk are the prime factors of n.

for example: \[ \phi(6) = 6 \times \left(1 - \frac{1}{2}\right) \times \left(1 - \frac{1}{3}\right) = 2\]

Now, if n is product of p and q where p and q are prime numbers then,

\[ \phi(n = p \times q ) = n \times \left(1 - \frac{1}{p}\right) \times \left(1 - \frac{1}{q}\right)\] \[ \phi(n) = (p \times q) \times \left(1 - \frac{1}{p}\right) \times \left(1 - \frac{1}{q}\right)\] \[ \phi(n) = (p \times q) \times \left(\frac{p-1}{p}\right) \times \left(\frac{q-1}{q}\right)\] \[ \phi(n) = (p-1) \times (q-1)\]

φ(p.q) = (p-1) × (q-1), if p and q are prime numbers.

But how to generate public key?

After calculating φ(n) = (p-1) × (q-1), We need to choose an integer e such that:

  • 2 < e < ϕ(n)
  • e is coprime with ϕ(n) i.e., gcd(e, φ(n)) = 1.

Common choices for e are small prime numbers, typically:

  • 3 (often used for efficiency reasons),
  • 65537 (a commonly used value that is prime and has a simple binary representation, making modular exponentiation faster).

Corresponding private key

After calculating e, we need to choose an integer d such that:

  • e × d ≡ 1 (mod ϕ(n))

What does e × d ≡ 1 mod ϕ(n) means?

The notation a ≡ b (modr) is defined to mean that r divides the difference a−b

For example,

  • 10 ≡ 0 mod 5
  • 11 ≡ 1 mod 5
• • •

Section 3: Implementing RSA on paper

Now Bob wants to send message=15 to Alice securely.

  • So, Alice comes with a plan and generates two large prime number say p = 11 and q = 13.
  • Now n = p × q = 11 × 13 = 143
  • Now φ(n) = (p-1) × (q-1) = 10 × 12 = 120
  • PUBLIC KEY: 2 < e < ϕ(n) & gcd(e, ϕ(n)) = 1, where ϕ(n) = 120
  • it implies that e belongs to {7, 11, ...}
  • let e = 7 be the PUBLIC KEY of Alice
  • Corresponding PRIVITE KEY: e × d ≡ 1 (mod ϕ(n)), where ϕ(n) = 120 and e = 7
  • d = 103 satisfy the given conditions.

Now how to encrypt and decrypt the data?

demo

demo

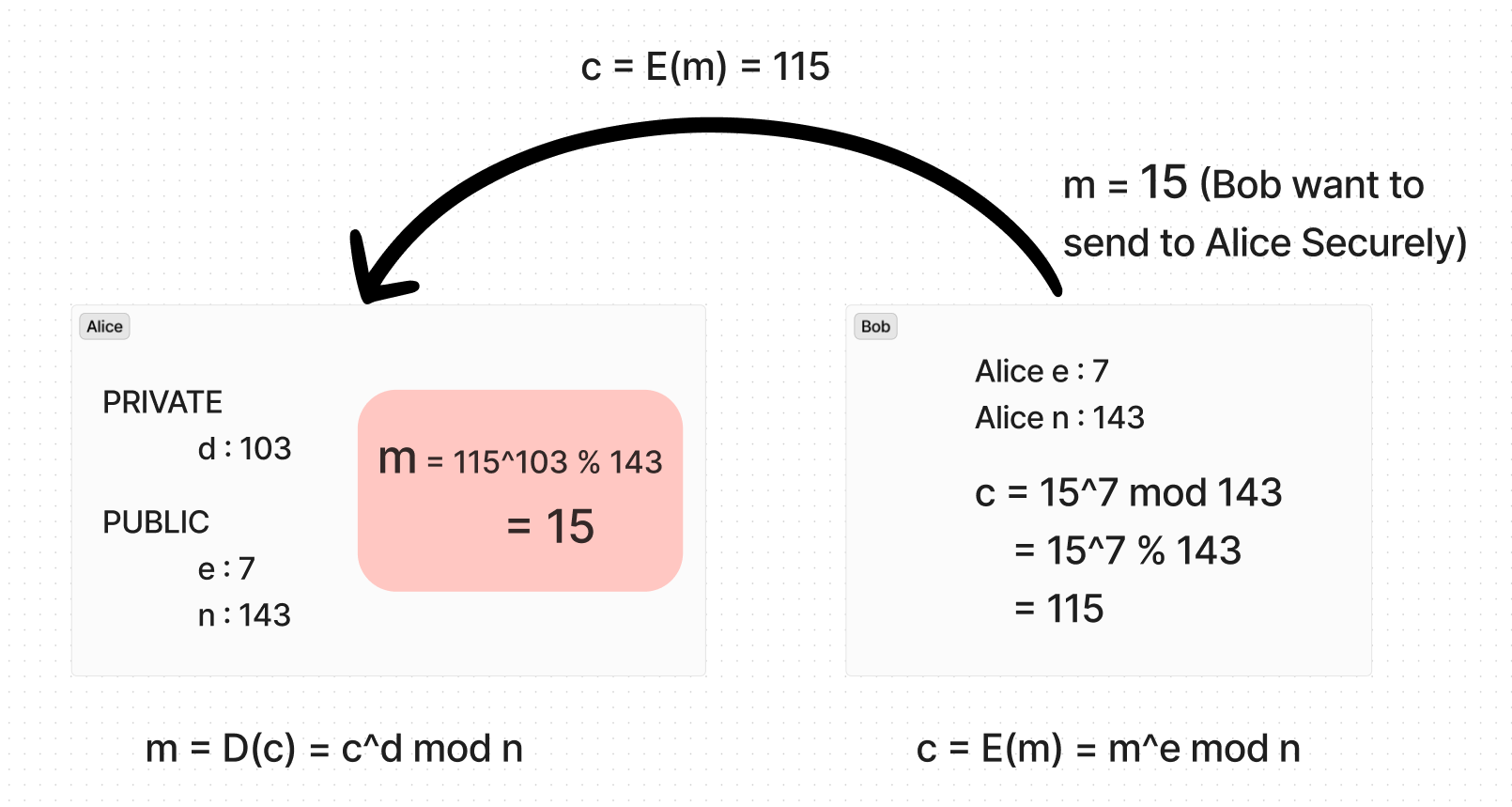
As Bob wants to send messages = 15 to Alice securely So he Encrypt it using the following function:

\[ E(m) = m^e \mod n \]

Now Bob have PUBLIC KEY of Alice i.e., e = 7 and n = 143

\[ c = E(15) = 15^7 \mod 143 \] \[ c = 17,08,59,375 \mod 143 \] \[ c = 115 \]

Now Bob Will Simply send c = 115 to Alice through Internet. But How will Alice Decode it? Alice will use his PRIVITE KEY to decrypt this message through the following function:

\[ D(c) = c^d \mod n \]

As you notice that this is same function which we use to encrypt the message but now we need to reverse the process and for this we Already generated modular inverse of e which is d.

\[ m = D(115) = 115^{103} \mod 143 \] \[ m = 115^{103} \mod 143 \] \[ m = 1.7859839693338012078403257027778e+212 \mod 143 \] \[ m = 15 \]

As you notice that this is same message which Bob want to send to Alice...

Section 4: Implementing RSA in Python

First we code some basic functions

Prime Number Generation

def is_prime(n:int)->bool:
    if n < 2: return False
    if n in (2, 3): return True
    if n % 2 == 0 or n % 3 == 0: return False
    i = 5
    while i * i <= n:
        if n % i == 0 or n % (i + 2) == 0: return False
        i += 6
    return True

def prime_number_greater_than(n:int)->int:
    while True:
        if is_prime(n): return n
        n+=1

def is_coprime(a:int, b:int)->bool:
    return gcd(a, b)==1

def is_integer(n:int)->bool:
    return n%1 == 0

GCD and Modular Inverse

def gcd(a:int, b:int)->int:
    # The Euclidean algorithm is based on the principle that the GCD of two numbers also divides their difference.
    while b:
        a, b = b, a % b
    return a

def extended_gcd(a: int, b: int):
    if a == 0:
        return b, 0, 1
    g, x1, y1 = extended_gcd(b % a, a)
    x = y1 - (b // a) * x1
    y = x1
    return g, x, y

def modular_inverse(e: int, phi: int) -> int:
    g, x, y = extended_gcd(e, phi)
    if g != 1:
        raise ValueError("modular inverse does not exist")
    else:
        return x % phi

Encryption and Decryption

def cryptor_raw(data:int, key:int, n:int)->int:
    assert data < n, "data must be less than n"
    result = 1  # Initialize result
    base = data % n  # Ensure base is in the correct range

    while key > 0:
        # If key is odd, multiply the base with the result
        if key % 2 == 1:
            result = (result * base) % n

        # Now key must be even, divide it by 2
        key = key // 2
        base = (base * base) % n  # Square the base and reduce it modulo n

    return result

class RSA:
    def __init__(self)->None:
        self.p = prime_number_greater_than(random.randint(1_000_000, 1_000_000_000))
        self.q = prime_number_greater_than(random.randint(1_000_000, 1_000_000_000))
        assert self.p != self.q
        self.n = self.p*self.q
        self.phi = (self.p-1)*(self.q-1)
        self.public_key = self.__public_key()
        self.private_key = self.__private_key()

    def __public_key(self)->int:
        # for e in [3, 5, 17, 257, 65537]:
            # if e < self.phi and is_coprime(e, self.phi): return e
        for e in range(2+1, self.phi):
            if is_coprime(e, self.phi): return e
        raise ValueError("Failed to find a valid public key")

    def __private_key(self)->int:
        return modular_inverse(self.public_key, self.phi)

    def __repr__(self) -> str:
        return (f"{self.__class__.__name__}(\n"
                f"    p={self.p},\n"
                f"    q={self.q},\n"
                f"    phi={self.phi},\n"
                f"    public_key={self.public_key},\n"
                f"    private_key={self.private_key},\n"
                f"    n={self.n}\n)")
    def decryptor_raw(self, data:int)->int:
        return cryptor_raw(data, self.private_key, self.n)

main function

def main()->None:
    server = RSA()
    print(server)
    server_pubkey = server.public_key
    server_n = server.n

    m = 999
    print(f"original message : {m}")
    c = cryptor_raw(m, key=server_pubkey, n=server_n)
    print(f"encrypted message : {c}")
    m = server.decryptor_raw(c)
    print(f"decrypted message : {m}")

if __name__ == "__main__":
    main()

output

RSA(
    p=653657353,
    q=27653137,
    phi=18075675652255872,
    public_key=5,
    private_key=7230270260902349,
    n=18075676333566361
)
original message : 999
encrypted message : 995009990004999
decrypted message : 999

additional methods to encrypt and decrypt bytesarray

def int_to_bytes(value, byte_size=255):
    """Convert an integer to a list of bytes, ensuring each byte is within the range 0-255."""
    bytes_list = []
    while value > 0:
        bytes_list.append(value % byte_size)
        value //= byte_size
    return bytes_list[::-1]  # Reverse the list to maintain the correct order

def cryptor(data:bytearray, key:int, n:int)->bytearray:
    result = []
    for i in data:
        encoded_value = cryptor_raw(i, key, n)
        encoded_bytes = int_to_bytes(encoded_value)
        result.append(len(encoded_bytes))  # Store the length of the encoded segment
        result.extend(encoded_bytes)
    return bytearray(result)

class RSA:
    ...

    def decryptor(self, data:bytearray)->bytearray:
        decrypted = []
        idx = 0
        while idx < len(data):
            segment_length = data[idx]
            idx += 1
            encoded_value = 0
            for j in range(segment_length):
                encoded_value = encoded_value * 255 + data[idx]
                idx += 1
            decrypted_value = self.decryptor_raw(encoded_value)
            decrypted.append(decrypted_value)
        return bytearray(decrypted)

def main()->None:
    server = RSA()
    print(server)
    server_pubkey = server.public_key
    server_n = server.n

    m = 999
    print(f"original message : {m}")
    c = cryptor_raw(m, key=server_pubkey, n=server_n)
    print(f"encrypted message : {c}")
    m = server.decryptor_raw(c)
    print(f"decrypted message : {m}")

    message = bytearray(b"My name is Laksh Kumar Sisodiya.")
    print(message)
    message_encrypted = cryptor(message, key=server_pubkey, n=server_n)
    print(message_encrypted)
    message_decrypted = server.decryptor(message_encrypted)
    print(message_decrypted)

if __name__ == "__main__":
    main()

output

RSA(
    p=287023507,
    q=798472933,
    phi=229180500388739592,
    public_key=5,
    private_key=91672200155495837,
    n=229180501474236031
)
original message : 999
encrypted message : 995009990004999
decrypted message : 999
bytearray(b'My name is Laksh Kumar Sisodiya.')
bytearray(b'\x04\xa3=\xd1\xd4\x05\x06"?\xe1\x97\x04\x02\x06\x06\x02\x05\x03\xceF\x81\xe6\x05\x02\x07\xe3"%\x05\x03\xa2\xeb^O\x05\x02{\xd8\xafe\x04\x02\x06\x06\x02\x05\x03\x04\xb4\x84Z\x05\x04\xc1\x05\x98s\x04\x02\x06\x06\x02\x04\x98\xe9\x15\xc4\x05\x02\x07\xe3"%\x05\x03P\xdb:\xa7\x05\x04\xc1\x05\x98s\x05\x02\xdf\xbeg\x86\x04\x02\x06\x06\x02\x04\x8f\x1d`-\x05\x05/<\x04W\x05\x03\xa2\xeb^O\x05\x02\x07\xe3"%\x05\x04\x8d0\xbd6\x04\x02\x06\x06\x02\x04\xed\x8eS5\x05\x03\x04\xb4\x84Z\x05\x04\xc1\x05\x98s\x05\x03\xfb<\x0b\xf6\x05\x02]\x16\x01F\x05\x03\x04\xb4\x84Z\x05\x06"?\xe1\x97\x05\x02\x07\xe3"%\x04\x0ckp\xf1')
bytearray(b'My name is Laksh Kumar Sisodiya.')

what next? Signatures

Private Key: The sender uses their private key to create the digital signature from the message or document.

Public Key: The recipient can verify the digital signature using the sender's public key. By comparing the digest derived from the received message with the decrypted digital signature using the public key, the recipient can confirm the authenticity and integrity of the message.

Full Code

you can download full code from my github account.

import random, math
from typing import Optional

def is_prime(n:int)->bool:
    # if n<2: return False
    # for i in range(2, math.floor(math.sqrt(n))+1): 
        # if(n % i == 0): return False
    # return True
    if n < 2: return False
    if n in (2, 3): return True
    if n % 2 == 0 or n % 3 == 0: return False
    i = 5
    while i * i <= n:
        if n % i == 0 or n % (i + 2) == 0: return False
        i += 6
    return True
def prime_number_greater_than(n:int)->int:
    while True:
        if is_prime(n): return n
        n+=1

def gcd(a:int, b:int)->int:
    # The Euclidean algorithm is based on the principle that the GCD of two numbers also divides their difference.
    while b:
        a, b = b, a % b
    return a
def is_coprime(a:int, b:int)->bool:
    return gcd(a, b)==1
def is_integer(n:int)->bool:
    return n%1 == 0

def extended_gcd(a: int, b: int):
    if a == 0:
        return b, 0, 1
    g, x1, y1 = extended_gcd(b % a, a)
    x = y1 - (b // a) * x1
    y = x1
    return g, x, y
def modular_inverse(e: int, phi: int) -> int:
    g, x, y = extended_gcd(e, phi)
    if g != 1:
        raise ValueError("modular inverse does not exist")
    else:
        return x % phi

def int_to_base255(n: int) -> list:
    if n == 0:
        return [0]

    digits = []
    while n:
        digits.append(n % 255)
        n //= 255

    return digits[::-1]  # Reverse the list to get the correct order
def base255_to_int(digits: list) -> int:
    n = 0
    for digit in digits:
        n = n * 255 + digit

    return n
def int_to_bytes(value, byte_size=255):
    """Convert an integer to a list of bytes, ensuring each byte is within the range 0-255."""
    bytes_list = []
    while value > 0:
        bytes_list.append(value % byte_size)
        value //= byte_size
    return bytes_list[::-1]  # Reverse the list to maintain the correct order

def split_into_chunks(lst, chunk_size=3):
    """Splits a list into chunks of specified size."""
    for i in range(0, len(lst), chunk_size):
        yield lst[i:i + chunk_size]

def cryptor_raw(data:int, key:int, n:int)->int:
    assert data < n, "data must be less than n"
    result = 1  # Initialize result
    base = data % n  # Ensure base is in the correct range

    while key > 0:
        # If key is odd, multiply the base with the result
        if key % 2 == 1:
            result = (result * base) % n

        # Now key must be even, divide it by 2
        key = key // 2
        base = (base * base) % n  # Square the base and reduce it modulo n

    return result
def cryptor(data:bytearray, key:int, n:int)->bytearray:
    # encoded = [cryptor_raw(base255_to_int(i), key, n) for i in split_into_chunks(data, chunk_size=1)]
    result = []
    for i in data:
        encoded_value = cryptor_raw(i, key, n)
        encoded_bytes = int_to_bytes(encoded_value)
        result.append(len(encoded_bytes))  # Store the length of the encoded segment
        result.extend(encoded_bytes)
    return bytearray(result)

class RSA:
    def __init__(self)->None:
        self.p = prime_number_greater_than(random.randint(1_000_000, 1_000_000_000))
        self.q = prime_number_greater_than(random.randint(1_000_000, 1_000_000_000))
        assert self.p != self.q
        self.n = self.p*self.q
        self.phi = (self.p-1)*(self.q-1)
        self.public_key = self.__public_key()
        self.private_key = self.__private_key()
    def __public_key(self):
        # for e in [3, 5, 17, 257, 65537]:
            # if e < self.phi and is_coprime(e, self.phi): return e
        for e in range(2+1, self.phi):
            if is_coprime(e, self.phi): return e
        raise ValueError("Failed to find a valid public key")
    def __private_key(self):
        return modular_inverse(self.public_key, self.phi)

    def __repr__(self) -> str:
        return (f"{self.__class__.__name__}(\n"
                f"    p={self.p},\n"
                f"    q={self.q},\n"
                f"    phi={self.phi},\n"
                f"    public_key={self.public_key},\n"
                f"    private_key={self.private_key},\n"
                f"    n={self.n}\n)")
    def decryptor_raw(self, data:int)->int:
        return cryptor_raw(data, self.private_key, self.n)
    def decryptor(self, data:bytearray)->bytearray:
        decrypted = []
        idx = 0
        while idx < len(data):
            segment_length = data[idx]
            idx += 1
            encoded_value = 0
            for j in range(segment_length):
                encoded_value = encoded_value * 255 + data[idx]
                idx += 1
            decrypted_value = self.decryptor_raw(encoded_value)
            decrypted.append(decrypted_value)
        return bytearray(decrypted)


if __name__ == "__main__":
    # client = RSA()
    # client_pubkey = client.public_key
    # client_n = client.n

    server = RSA()
    print(server)
    server_pubkey = server.public_key
    server_n = server.n

    m = 999
    print(f"original message : {m}")
    c = cryptor_raw(m, key=server_pubkey, n=server_n)
    print(f"encrypted message : {c}")
    m = server.decryptor_raw(c)
    print(f"decrypted message : {m}")


    # client want to send to server
    message = bytearray(b"My name is Laksh Kumar Sisodiya.")
    print(message)
    message_encrypted = cryptor(message, key=server_pubkey, n=server_n)
    print(message_encrypted)
    message_decrypted = server.decryptor(message_encrypted)
    print(message_decrypted)

    # handshake ig signature ...
ThefCraft

Written by ThefCraft

Explore the dynamic fusion of mathematics and computing through the eyes of ThefCraft, a B.Tech. student at IIT Patna. Delve into the depths of algorithms, data analysis, artificial intelligence, deep learning and computational techniques in this captivating blog. Join ThefCraft on a journey of innovation and discovery at the intersection of two powerful disciplines.