Mastering Linear Regression: From Scratch without Gradient Descent.

Introduction

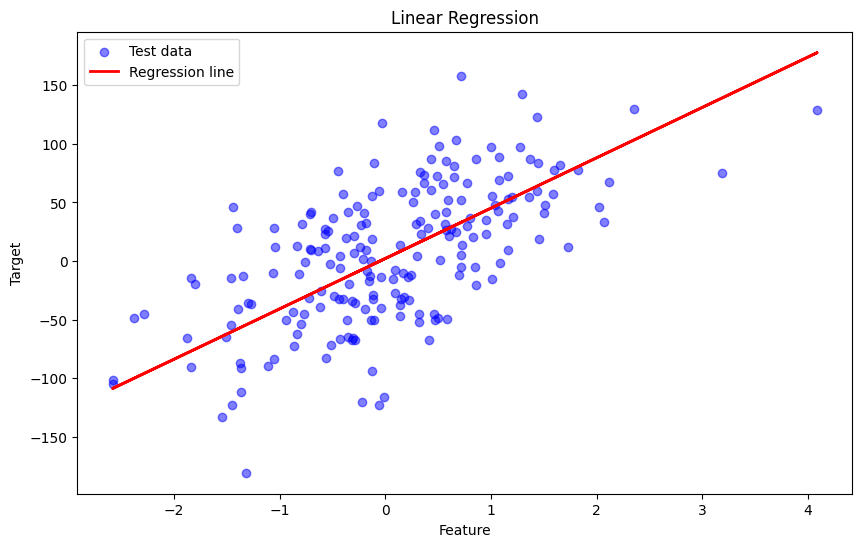
Linear Regression is a method in which we tries to best-fit a line on the dataset in a way that that minimizes the mean square error. In other words Linear Regression is a method used to define a relationship between a dependent variable (Y) and independent variables (x1, x2, ..., xk). Which is simply written as :

\[ \hat{y} = {m_1}\times{x_1} + {m_2}\times{x_2} + \ldots + {m_k}\times{x_k} + b \] or simply \[ \hat{y} = {M}{X} + b \]

where:

• ŷ is the predicted value (dependent variable).
• X is the independent variables.
• M is the slope of the line (weights).
• b is the y-intercept (bias).

Example Scenario

Imagine we wants to predict the house price based on some parameters like rooms and area etc. Then we could establish a relationship between its price and the input parameters using linear regression algorithm.

Section 2: Mathematical Foundations

Mean Squared Error (MSE)

To measure the error of our linear regression model, we use the Mean Squared Error (MSE), which calculates the mean of the squared difference between the actual and predicted values:

\[ \text{MSE} = \frac{1}{n} \sum_{i=1}^{n} (y_i - \hat{y_i})^2 \]

where:

• n is the number of data points.
• y𝒊 is the actual value.
• ŷ𝒊 is the predicted value.

On Now you know what mean squared error is but we want to minimize this error to accurately fit the line on the data points. but how to minimize this error?

Finding Minima using Derivatives

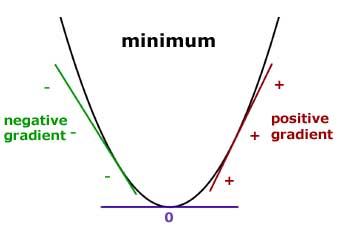
In a smoothly changing function a minimum is always where the function flattens out (except for a saddle point).

Partial Derivatives

The partial derivatives of the MSE with respect to m:

\[ \frac{\partial \text{MSE}}{\partial m} = \frac{1}{n} \sum_{i=1}^{n} (y_i - \hat{y_i})^2 \] \[ \frac{\partial \text{MSE}}{\partial m} = \frac{1}{n} \sum_{i=1}^{n} (y_i - (m {x_i} + b))^2 \] \[ \frac{\partial \text{MSE}}{\partial m} = \frac{1}{n} \sum_{i=1}^{n} (y_i - (m {x_i} + b))(-2{x_i}) \] \[ \frac{\partial \text{MSE}}{\partial m} = -\frac{2}{n} \sum_{i=1}^{n} x_i (y_i - (m {x_i} + b)) \] \[ \frac{\partial \text{MSE}}{\partial m} = -\frac{2}{n} \sum_{i=1}^{n} x_i (y_i - \hat{y_i}) \]

The partial derivatives of the MSE with respect to b:

\[ \frac{\partial \text{MSE}}{\partial b} = \frac{1}{n} \sum_{i=1}^{n} (y_i - \hat{y_i})^2 \] \[ \frac{\partial \text{MSE}}{\partial b} = \frac{1}{n} \sum_{i=1}^{n} (y_i - (m {x_i} + b))^2 \] \[ \frac{\partial \text{MSE}}{\partial b} = \frac{1}{n} \sum_{i=1}^{n} (y_i - (m {x_i} + b))(-2) \] \[ \frac{\partial \text{MSE}}{\partial b} = -\frac{2}{n} \sum_{i=1}^{n} (y_i - (m {x_i} + b)) \] \[ \frac{\partial \text{MSE}}{\partial b} = -\frac{2}{n} \sum_{i=1}^{n} (y_i - \hat{y_i}) \]

Equating the gradients of the error function to zero

Equating the partial derivatives of the MSE with respect to b to zero:

\[ \frac{\partial \text{MSE}}{\partial b} = -\frac{2}{n} \sum_{i=1}^{n} (y_i - (m {x_i} + b)) = 0 \] \[ -\frac{2}{n} \sum_{i=1}^{n} (y_i - m {x_i} - b) = 0 \] \[ -\frac{2}{n} \sum_{i=1}^{n} (y_i) +\frac{2}{n} \sum_{i=1}^{n} ( m {x_i} ) +\frac{2}{n} \sum_{i=1}^{n} (b) = 0 \] \[ -\frac{1}{n} \sum_{i=1}^{n} (y_i) +\frac{1}{n} \sum_{i=1}^{n} ( m {x_i} ) +\frac{1}{n} \sum_{i=1}^{n} (b) = \frac{0}{2} \] \[ -\frac{1}{n} \sum_{i=1}^{n} y_i +\frac{m}{n} \sum_{i=1}^{n} {x_i} + b = 0 \] \[ -\overline{y} + m \times \overline{x} + b = 0 \hspace{10mm} \ldots (1) \]

Equating the partial derivatives of the MSE with respect to m to zero:

\[ \frac{\partial \text{MSE}}{\partial m} = -\frac{2}{n} \sum_{i=1}^{n} x_i (y_i - (m {x_i} + b)) = 0 \] \[ -\frac{2}{n} \sum_{i=1}^{n} (x_i \times y_i - x_i \times (m {x_i} + b)) = 0 \] \[ -\frac{2}{n} \sum_{i=1}^{n} (x_i y_i - m {x_i}^2 - x_i b) = 0 \] \[ -\frac{1}{n} \sum_{i=1}^{n} (x_i y_i - m {x_i}^2 - x_i b) = \frac{0}{2} \] \[ -\frac{1}{n} \sum_{i=1}^{n} (x_i y_i) +\frac{1}{n} \sum_{i=1}^{n} (m {x_i}^2) +\frac{1}{n} \sum_{i=1}^{n} (x_i b) = 0 \] \[ -\overline{xy} + m \times \overline{x^2} + b \times \overline{x} = 0 \hspace{10mm} \ldots (2) \]

Now we have two equations and two equations so now solving them together

using equation one we have \[ -\overline{y} + m \times \overline{x} + b = 0 \] \[ b = \overline{y} - m \times \overline{x} \] puting this value of b in equation two we have \[ -\overline{xy} + m \times \overline{x^2} + b \times \overline{x} = 0 \] \[ -\overline{xy} + m \times \overline{x^2} + (\overline{y} - m \times \overline{x}) \times \overline{x} = 0 \] \[ -\overline{xy} + m \times \overline{x^2} + \overline{y} \times \overline{x} - m{\overline{x}}^2 = 0 \] \[ -\overline{xy} + \overline{y} \times \overline{x} + m (\overline{x^2} - {\overline{x}}^2) = 0 \] \[ m (\overline{x^2} - {\overline{x}}^2) = \overline{xy} - \overline{y} \times \overline{x} \] \[ m (\frac{1}{n} \sum_{i=1}^{n} x_i^2 - (\frac{1}{n} \sum_{i=1}^{n} x_i)^2) = \frac{1}{n} \sum_{i=1}^{n} x_i y_i - \frac{1}{n} \sum_{i=1}^{n} y_i \times \frac{1}{n} \sum_{i=1}^{n} x_i \] \[ mn^2 (\frac{1}{n} \sum_{i=1}^{n} x_i^2 - (\frac{1}{n} \sum_{i=1}^{n} x_i)^2) = n \sum_{i=1}^{n} x_i y_i - \sum_{i=1}^{n} y_i \times \sum_{i=1}^{n} x_i \] \[ m (n \sum_{i=1}^{n} x_i^2 - n^2(\frac{1}{n} \sum_{i=1}^{n} x_i)^2) = n \sum_{i=1}^{n} x_i y_i - \sum_{i=1}^{n} y_i \sum_{i=1}^{n} x_i \] \[ m (n \sum_{i=1}^{n} x_i^2 - (\sum_{i=1}^{n} x_i)^2) = n \sum_{i=1}^{n} x_i y_i - \sum_{i=1}^{n} y_i \sum_{i=1}^{n} x_i \] \[ m (n \sum_{}^{} x^2 - (\sum_{}^{} x)^2) = n \sum_{}^{} x y - \sum_{}^{} y \sum_{}^{} x \] \[ m = \frac{n \sum_{}^{} x y - \sum_{}^{} x \sum_{}^{} y}{n \sum_{}^{} x^2 - (\sum_{}^{} x)^2} \]

Now using equation two we have

\[ -\overline{xy} + m \times \overline{x^2} + b \times \overline{x} = 0 \] \[ m \times \overline{x^2} = \overline{xy} - b \times \overline{x} \] \[ m = (\overline{xy} - b \times \overline{x})/(\overline{x^2}) \]

on puting this value of m in equation one we have

\[ -\overline{y} + m \times \overline{x} + b = 0 \] \[ -\overline{y} + (\overline{xy} - b \times \overline{x})/(\overline{x^2}) \times \overline{x} + b = 0 \] \[ -\overline{y} \times \overline{x^2} + (\overline{xy} - b \times \overline{x}) \times \overline{x} + b \times \overline{x^2} = 0 \] \[ -\overline{y} \times \overline{x^2} + \overline{xy} \times \overline{x} - b \times \overline{x} \times \overline{x} + b \times \overline{x^2} = 0 \] \[ -\overline{y} \times \overline{x^2} + \overline{xy} \times \overline{x} + b (\overline{x^2} - \overline{x} \times \overline{x}) = 0 \] \[ b (\overline{x^2} - \overline{x} \times \overline{x}) = \overline{y} \times \overline{x^2} - \overline{xy} \times \overline{x} \] \[ b (\overline{x^2} - {\overline{x}}^2) = \overline{y} \times \overline{x^2} - \overline{xy} \times \overline{x} \] \[ b (\frac{1}{n} \sum_{}^{} x^2 - (\frac{1}{n} \sum_{}^{} x)^2) = \frac{1}{n} \sum_{}^{} y \times \frac{1}{n} \sum_{}^{} x^2 - \frac{1}{n} \sum_{}^{} xy \times \frac{1}{n} \sum_{}^{} x \] \[ bn^2 (\frac{1}{n} \sum_{}^{} x^2 - (\frac{1}{n} \sum_{}^{} x)^2) = \sum_{}^{} y \times \sum_{}^{} x^2 - \sum_{}^{} xy \times \sum_{}^{} x \] \[ b(n \sum_{}^{} x^2 - n^2(\frac{1}{n} \sum_{}^{} x)^2) = \sum_{}^{} y \sum_{}^{} x^2 - \sum_{}^{} xy \sum_{}^{} x \] \[ b(n \sum_{}^{} x^2 - (\sum_{}^{} x)^2) = \sum_{}^{} y \sum_{}^{} x^2 - \sum_{}^{} xy \sum_{}^{} x \] \[ b = \frac{\sum_{}^{} y \sum_{}^{} x^2 - \sum_{}^{} xy \sum_{}^{} x}{n \sum_{}^{} x^2 - (\sum_{}^{} x)^2} \]

For line y = ax + b

We just derive the linear regression formula which you use in your physics labs. But this is just for one dimensional feature vector. But don't worry we can easily modify this for linear regression of n dimensional feature vector.

Section 3: Python Implementation Up to This point

import numpy as np
from sklearn.datasets import make_regression
from sklearn.model_selection import train_test_split
from sklearn.metrics import mean_squared_error, r2_score

X, Y = make_regression(n_samples=10000, n_features=1, noise=50)
X = X.reshape(-1)
X_train, X_test, Y_train, Y_test = train_test_split(X, Y, test_size=0.2)
def fit(X, Y):
    assert len(X.shape) == len(Y.shape) and len(X.shape) == 1, "X and Y must one dimensional i.e., (n, )"
    n=len(X)   
    sum_y = Y.sum()
    sum_x = X.sum()
    sum_xy = (X*Y).sum()
    sum_xx = (X*X).sum()
    m = (n*sum_xy - sum_x*sum_y)/(n*sum_xx-sum_x*sum_x)
    b = (sum_y*sum_xx - sum_xy*sum_x)/(n*sum_xx-sum_x*sum_x)
    return lambda x: m*x+b
model = fit(X_train, Y_train)

predictions = model(X_test)
print(f"MSE: {mean_squared_error(predictions, Y_test):.5f}")
print(f"R^2 Score: {r2_score(predictions, Y_test):.5f}")

from sklearn import linear_model
sklearn_model = linear_model.LinearRegression()
X_train = X_train.reshape(-1, 1)
X_test = X_test.reshape(-1, 1)
sklearn_model.fit(X_train, Y_train)
sklearn_predictions = sklearn_model.predict(X_test)
print(f"sklearn MSE: {mean_squared_error(sklearn_predictions, Y_test):.5f}")
print(f"sklearn R^2 Score: {r2_score(sklearn_predictions, Y_test):.5f}")

Output:

MSE: 2333.91338
R^2 Score: -3.07210
sklearn MSE: 2333.91338
sklearn R^2 Score: -3.07210

Section 4: Linear Regression for multiple variables

Now we have new linear regression formula i.e.,

\[ \hat{y} = {M}{X} + b \] or \[ \hat{y} = m_1 x_1 + m_2 x_2 + \ldots + m_j x_j + b \] \[ \hat{y} = b + \sum_{i=1}^{n} {m_j} {x_j} \]

Again Doing Partial Derivatives

The partial derivatives of the MSE with respect to b:

\[ \frac{\partial \text{MSE}}{\partial b} = \frac{1}{n} \sum_{i=1}^{n} (y_i - \hat{y_i})^2 \] \[ \frac{\partial \text{MSE}}{\partial b} = \frac{1}{n} \sum_{i=1}^{n} (y_i - (b + \sum_{}^{} {m_j} {x_ij}))^2 \] \[ \frac{\partial \text{MSE}}{\partial b} = \frac{1}{n} \sum_{i=1}^{n} (y_i - (b + \sum_{}^{} {m_j} {x_ij}))(-2) \] \[ \frac{\partial \text{MSE}}{\partial b} = -\frac{2}{n} \sum_{i=1}^{n} (y_i - (b + \sum_{}^{} {m_j} {x_ij})) \] \[ \frac{\partial \text{MSE}}{\partial b} = -\frac{2}{n} \sum_{i=1}^{n} (y_i - \hat{y_i}) \]

The partial derivatives of the MSE with respect to mj:

\[ \frac{\partial \text{MSE}}{\partial m_j} = \frac{1}{n} \sum_{i=1}^{n} (y_i - \hat{y_i})^2 \] \[ \frac{\partial \text{MSE}}{\partial m_j} = \frac{1}{n} \sum_{i=1}^{n} (y_i - (b + \sum_{}^{} {m_j} {x_ij}))^2 \] \[ \frac{\partial \text{MSE}}{\partial m_j} = \frac{1}{n} \sum_{i=1}^{n} (y_i - (b + \sum_{}^{} {m_j} {x_ij}))(-2{x_ij}) \] \[ \frac{\partial \text{MSE}}{\partial m_j} = -\frac{2}{n} \sum_{i=1}^{n} x_ij (y_i - (b + \sum_{}^{} {m_j} {x_ij})) \] \[ \frac{\partial \text{MSE}}{\partial m_j} = -\frac{2}{n} \sum_{i=1}^{n} x_ij (y_i - \hat{y_i}) \]

Again Equating the gradients of the error function to zero

Lets assume that we have k dimensional feature vector.

Equating the partial derivatives of the MSE with respect to b to zero:

\[ \frac{\partial \text{MSE}}{\partial b} = -\frac{2}{n} \sum_{i=1}^{n} (y_i - (b + \sum_{}^{} {m_j} {x_ij})) = 0 \] \[ -\frac{1}{n} \sum_{i=1}^{n} (y_i - b - \sum_{}^{} {m_j} {x_ij}) = \frac{0}{2} \] \[ -\frac{1}{n} \sum_{i=1}^{n} (y_i - b - \sum_{}^{} {m_j} {x_ij}) = 0 \] \[ -\frac{1}{n} \sum_{i=1}^{n} y_i + \frac{1}{n} \sum_{i=1}^{n} b + \frac{1}{n} \sum_{i=1}^{n} (\sum_{}^{} {m_j} {x_ij}) = 0 \] \[ -\overline{y} + b + \frac{1}{n} \sum_{i=1}^{n} (\sum_{}^{} {m_j} {x_ij}) = 0 \] \[ -\overline{y} + b + \frac{1}{n} \sum_{i=1}^{n} (m_1 x_i1 + m_2 x_i2 + \ldots + m_j x_ij) = 0 \] \[ -\overline{y} + b + (\frac{1}{n} \sum_{i=1}^{n} m_1 x_i1 + \frac{1}{n} \sum_{i=1}^{n} m_2 x_i2 + \ldots + \frac{1}{n} \sum_{i=1}^{n} m_j x_ij) = 0 \] \[ -\overline{y} + b + (m_1 \overline{x_i1} + m_2 \overline{x_i2} + \ldots + m_j \overline{x_ij}) = 0 \] \[ -\overline{y} + b + \sum_{j=1}^{k}(m_j \overline{x_ij}) = 0 \hspace{10mm} \ldots (3) \]

Equating the partial derivatives of the MSE with respect to mj' to zero:

\[ \frac{\partial \text{MSE}}{\partial m_j*} = -\frac{2}{n} \sum_{i=1}^{n} x_ij' (y_i - (b + \sum_{}^{} {m_j} {x_ij})) = 0 \] \[ -\frac{1}{n} \sum_{i=1}^{n} x_ij' (y_i - b - \sum_{}^{} {m_j} {x_ij}) = \frac{0}{2} \] \[ -\frac{1}{n} \sum_{i=1}^{n} x_ij' (y_i - b - \sum_{}^{} {m_j} {x_ij}) = 0 \] \[ -\frac{1}{n} \sum_{i=1}^{n} x_ij' y_i + \frac{1}{n} \sum_{i=1}^{n} x_ij' b + \frac{1}{n} \sum_{i=1}^{n} (x_ij' \sum_{}^{} {m_j} {x_ij}) = 0 \] \[ -\overline{x_ij' y_i} + b \overline{x_ij'} + \frac{1}{n} \sum_{i=1}^{n} (x_ij' \sum_{}^{} {m_j} {x_ij}) = 0 \] \[ -\overline{x_ij' y_i} + b \overline{x_ij'} + \frac{1}{n} \sum_{i=1}^{n} (x_ij' \times (m_1 x_i1 + m_2 x_i2 + \ldots + m_j x_ij)) = 0 \] \[ -\overline{x_ij' y_i} + b \overline{x_ij'} + \frac{1}{n} \sum_{i=1}^{n} (x_ij' \times m_1 x_i1 + x_ij' \times m_2 x_i2 + \ldots + x_ij' \times m_j x_ij) = 0 \] \[ -\overline{x_ij' y_i} + b \overline{x_ij'} + (\frac{1}{n} \sum_{i=1}^{n} x_ij' m_1 x_i1 + \frac{1}{n} \sum_{i=1}^{n} x_ij' m_2 x_i2 + \ldots + \frac{1}{n} \sum_{i=1}^{n} x_ij' m_j x_ij) = 0 \] \[ -\overline{x_ij' y_i} + b \overline{x_ij'} + (m_1 \overline{x_ij' x_i1} + m_2 \overline{x_ij' x_i2} + \ldots + m_j \overline{x_ij' x_ij}) = 0 \] \[ -\overline{x_ij' y_i} + b \overline{x_ij'} + \sum_{j=1}^{k} (m_j \overline{x_ij' x_ij}) = 0 \hspace{10mm} \ldots (4) \]

using equation 3 we have

\[ -\overline{y} + b + \sum_{j=1}^{k}(m_j \overline{x_ij}) = 0 \] \[ b = \overline{y} - \sum_{j=1}^{k}(m_j \overline{x_ij}) \] on puting this value of b in equation 4 we have \[ -\overline{x_ij' y_i} + b \overline{x_ij'} + \sum_{j=1}^{k} (m_j \overline{x_ij' x_ij}) = 0\] \[ -\overline{x_ij' y_i} + (\overline{y} - \sum_{j=1}^{k}(m_j \overline{x_ij})) \times \overline{x_ij'} + \sum_{j=1}^{k} (m_j \overline{x_ij' x_ij}) = 0\] \[ -\overline{x_ij' y_i} + \overline{y} \times \overline{x_ij'} - \overline{x_ij'} \times \sum_{j=1}^{k}(m_j \overline{x_ij}) + \sum_{j=1}^{k} (m_j \overline{x_ij' x_ij}) = 0\] \[ -\overline{x_ij' y_i} + \overline{y} \times \overline{x_ij'} - \sum_{j=1}^{k}(\overline{x_ij'} m_j \overline{x_ij}) + \sum_{j=1}^{k} (m_j \overline{x_ij' x_ij}) = 0\] \[ -\overline{x_ij' y_i} + \overline{y} \times \overline{x_ij'} - \sum_{j=1}^{k}(\overline{x_ij'} m_j \overline{x_ij} - m_j \overline{x_ij' x_ij}) = 0\] \[ -\overline{x_ij' y_i} + \overline{y} \times \overline{x_ij'} - \sum_{j=1}^{k} m_j (\overline{x_ij'} \times \overline{x_ij} - \overline{x_ij' x_ij}) = 0\] \[ \sum_{j=1}^{k} m_j (\overline{x_ij'} \times \overline{x_ij} - \overline{x_ij' x_ij}) = \overline{y} \times \overline{x_ij'} - \overline{x_ij' y_i} \] \[ \sum_{j=1}^{k} m_j (\overline{x_ij'} \times \overline{x_ij}) - \sum_{j=1}^{k} m_j (\overline{x_ij' x_ij}) = \overline{y} \times \overline{x_ij'} - \overline{x_ij' y_i} \] Now we have k such equation \[ \sum_{j=1}^{k} m_j (\overline{x_i1} \times \overline{x_ij}) - \sum_{j=1}^{k} m_j (\overline{x_i1 x_ij}) = \overline{y} \times \overline{x_i1} - \overline{x_i1 y_i} \] \[ \sum_{j=1}^{k} m_j (\overline{x_i2} \times \overline{x_ij}) - \sum_{j=1}^{k} m_j (\overline{x_i2 x_ij}) = \overline{y} \times \overline{x_i2} - \overline{x_i2 y_i} \] \[ \ldots \] \[ \ldots \] \[ \ldots \] \[ \sum_{j=1}^{k} m_j (\overline{x_ij'} \times \overline{x_ij}) - \sum_{j=1}^{k} m_j (\overline{x_ij' x_ij}) = \overline{y} \times \overline{x_ij'} - \overline{x_ij' y_i} \]

Now, We have k equations and k unknown variables so we can find the unknown variables using equation 3 and equations 4.

Python Implementation

import numpy as np
from sklearn.datasets import make_regression
from sklearn.model_selection import train_test_split
from sklearn.metrics import mean_squared_error, r2_score

X, Y = make_regression(n_samples=10000, n_features=5, noise=50)
X_train, X_test, Y_train, Y_test = train_test_split(X, Y, test_size=0.2)
def fit(X:np.ndarray, Y:np.ndarray):
    n=len(X)
    avg_y = Y.mean()
    avg_xj = X.mean(axis=0)
    avg_yxj = np.mean(Y.reshape(-1, 1) * X, axis=0) # np.mean(Y[:, np.newaxis] * X, axis=0)

    avg_xjxj = np.dot(X.T, X) / n

    B = avg_y * avg_xj - avg_yxj # shape = (k)
    A = np.outer(avg_xj, avg_xj) - avg_xjxj # shape = (k, k)
    M = np.linalg.solve(A, B)
    b = avg_y - np.dot(M, avg_xj) # avg_y - (avg_xj * M).sum() 
    return M, b

M, b = fit(X_train, Y_train)
model = lambda X: np.dot(X, M) + b
predictions = model(X_test)
print(f"MSE: {mean_squared_error(predictions, Y_test):.5f}")
print(f"R^2 Score: {r2_score(predictions, Y_test):.5f}")

from sklearn import linear_model
sklearn_model = linear_model.LinearRegression()
sklearn_model.fit(X_train, Y_train)
sklearn_predictions = sklearn_model.predict(X_test)
print(f"sklearn MSE: {mean_squared_error(sklearn_predictions, Y_test):.5f}")
print(f"sklearn R^2 Score: {r2_score(sklearn_predictions, Y_test):.5f}")

Output:

MSE: 2649.37218
R^2 Score: 0.79578
sklearn MSE: 2649.37218
sklearn R^2 Score: 0.79578

How I efficiently calculate A

\[ \sum_{j=1}^{k} m_j (\overline{x_i1} \times \overline{x_ij}) - \sum_{j=1}^{k} m_j (\overline{x_i1 x_ij}) = \overline{y} \times \overline{x_i1} - \overline{x_i1 y_i} \] \[ \sum_{j=1}^{k} m_j (\overline{x_i2} \times \overline{x_ij}) - \sum_{j=1}^{k} m_j (\overline{x_i2 x_ij}) = \overline{y} \times \overline{x_i2} - \overline{x_i2 y_i} \] \[ \ldots \] \[ \ldots \] \[ \ldots \] \[ \sum_{j=1}^{k} m_j (\overline{x_ij'} \times \overline{x_ij}) - \sum_{j=1}^{k} m_j (\overline{x_ij' x_ij}) = \overline{y} \times \overline{x_ij'} - \overline{x_ij' y_i} \]

For A (left side equation)

I calculate the first summation using np.outer(avg_xj, avg_xj)

Then calculate the second summation using avg_xjxj = np.dot(X.T, X) / n

Heres how i calculate it using an example where X have (n=2, k=3) shape

We Wants to calculate the following matrix

$$\begin{pmatrix}(x_11 x_11 + x_21 x_21) & (x_11 x_12 + x_21 x_22) & (x_11 x_13 + x_21 x_23)\\\ (x_12 x_11 + x_22 x_21) & (x_12 x_12 + x_22 x_22) & (x_12 x_13 + x_22 x_23)\\\ (x_13 x_11 + x_23 x_21) & (x_13 x_12 + x_23 x_22) & (x_13 x_13 + x_23 x_23)\end{pmatrix}$$ Or $$\begin{pmatrix}x_11 & x_21 \\\ x_12 & x_22 \\\ x_13 & x_23 \end{pmatrix} \times \begin{pmatrix}x_11 & x_12 & x_13 \\\ x_21 & x_22 & x_23 \end{pmatrix}$$

Then i subtract it from the first summation.

For B (right side equation)

I simply use the same expression avg_y * avg_xj - avg_yxj

Now i solve the System of linear equations

Now i solve the system of linear equations using np.linalg.solve(A, B) Which gives the slope of the linear regression.

find the intercept

To find the b i just use the same expression avg_y - (avg_xj * M).sum() but in optimized way avg_y - np.dot(M, avg_xj).

\[ b = \overline{y} - \sum_{j=1}^{k}(m_j \overline{x_ij}) \]

Full Code

you can download full code from my github account.